二进制

计算机由数字电路搭建而成，数字电路中只有 0 和 1 两种状态。

一位全加器（1-bit Full Adder）：

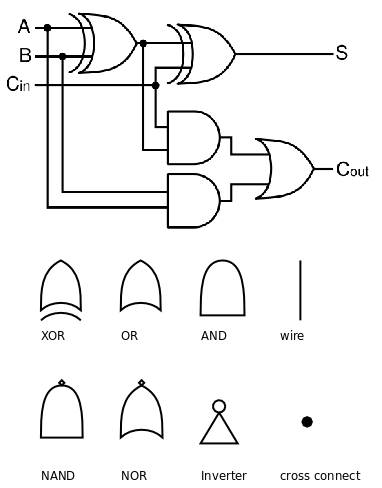
  • 逻辑电路由门电路（Gate）和导线（Wire）组成，同一条导线上在某一时刻的电压值只能是高和低两种状态之一，分别用 0 和 1 表示。
  • 如果两条导线短接在一起则它们的电压值相同，在接点处画一个黑点，如果接点处没有画黑点则表示这两条线并没有短接在一起，只是在画图时无法避免交叉。
  • 导线的电压值进入门电路的输入端，经过逻辑运算后在门电路的输出端输出运算结果的电压值。
  • 任何复杂的加减乘除运算都可以分解成简单的逻辑运算。
    • AND、OR 和 NOT 这三种逻辑运算分别用与门、或门和反相器（Inverter）实现。
      • 与非（NAND）和或非（NOR）运算就是在与、或运算的基础上取反。
      • 如果把与门、或门和反相器组合来实现 NAND 和 NOR 运算，电路会过于复杂，因此逻辑电路中通常有专用的与非门和或非门。
    • 异或（XOR，eXclusive OR）：两个操作数相同则结果为 0，两个操作数不同则结果为 1。
  • 图中，A、B 是两个加数，$$C_{in}$$ 是低位传上来的进位（Carry），相当于三个加数求和。
    • 三个加数都是 0 则结果为 0。
    • 三个加数都是 1 则结果为 11，即输出位 S 是 1，产生的进位 $$C_{out}$$ 也是 1。

把很多个一位全加器串接起来就成了多位加法器：

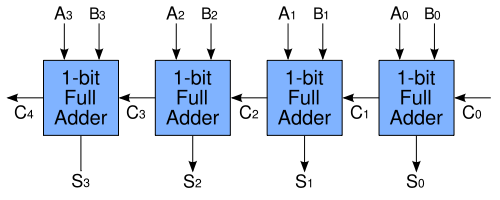
  • 4-bit ripple carry adder.
  • 上一级全加器的 $$C_{out}$$ 连接到下一级全加器的 $$C_{in}$$，让进位像涟漪一样一级一级传开，所以叫做 Ripple Carry Adder。
    • 这样的加法器可以把两个 4 bit 二进制数 $$A_3A_2A_1A_0$$ 和 $$B_3B_2B_1B_0$$ 加起来了。
    • 采用 Ripple Carry Adder 的加法器效率很低，只能加完了一位再加下一位，更实用、更复杂的加法器可以多个位一起计算。

进制转换

十进制：$$123=1×10^2+2×10^1+3×10^0$$

二进制换算成十进制：$$(A_3A_2A_1A_0)_2=A_3×2^3+A_2×2^2+A_1×2^1+A_0×2^0$$

  • 最左边的 $$A_3$$ 位称为最高位（MSB，Most Significant Bit），最右边的 $$A_0$$ 位称为最低位（LSB，Least Significant Bit）。

十进制换算成二进制可以采用除二反序取余法。

八进制和十六进制是程序员为了书写二进制方便而发明的简便写法。

整数的加减运算

概念：

  • 机器数：一个数在计算机中的二进制表示，带符号。

  • 真值：机器数对应的真正的数值。

  • 原码：符号位 + 真值绝对值。

    • 原码若用于有负数参与的加法运算会得到结果错误。

      
 00010000   (16)            10001000    (-8)
+10001000   (-8)           +10001000    (-8)
---------                  ---------
 10011000   (-24 wrong)     00010000    (16 wrong)
      • 加法规则不适用于有负数参与的加法，因此必须制定两套运算规则，意味着必须设计两种电路。

  • 反码

    • 正数反码即正数本身。
    • 负数反码是其原码的符号位以外的各位逐位取反；或是描述为该负数的绝对值（即对应的正数）的原码的每一个二进制位都取反。
    
 00010000   (16 的反码)            11110111    (-8 的反码)
+11110111   (-8 的反码)           +11110111    (-8 的反码)
---------                        ---------
 00000111   (just wrong)          11111000    (just wrong)

Sign and Magnitude 表示法

要用 8 个 bit 表示正数和负数，Sign and Magnitude 表示法把最高位规定为符号位（Sign Bit），0 表示正 1 表示负，剩下的 7 位表示绝对值的大小。

  • 例如 -1 表示成 10000001，+1 表示成 00000001。这样用 8 个 bit 表示整数的取值范围是 $$-2^7-1$$~$$2^7-1$$，即 -127~127。

采用这种表示法，计算机做加法运算需要处理以下逻辑：

  1. 如果两数符号位相同，就把它们的低 7 位相加，符号位不变。
    • 如果低 7 位相加时在最高位产生进位，说明结果的绝对值大于 127，超出 7 位所能表示的数值范围，称为溢出（Overflow）；这时通常用计算机中的一个标志位置来表示当前运算产生了溢出。
  2. 如果两数符号位不同，首先比较它们的低 7 位谁大，然后用大数减小数，结果的符号位和大数相同。
    • 减法可以转换成加法来计算，要计算 $$a-b$$，可以先把 $$b$$ 变号然后和 $$a$$ 相加，相当于计算 $$a+(-b)$$；此时如果两个加数的符号位不同，就要用大数的绝对值减小数的绝对值，这一步减法计算仍然避免不了。
    • 加法要进位，减法要借位，两者的计算过程不同，因此除了加法器电路之外，还要另外有一套减法器电路。

采用 Sign and Magnitude 表示法的缺点：

  • 计算机做加减运算需要处理很多逻辑，如比较符号位、比较绝对值、加法改减法、减法改加法、小数减大数改成大数减小数等等，非常低效。
  • 0 的表示不唯一，既可以表示成 10000000 也可以表示成 00000000，进一步增加了逻辑的复杂性。

1’s Complement 表示法

$$167-52=167+(-52)=167+(999-52)-1000+1=167+947-1000+1=1114-1000+1=114+1=115$$

  • $$167-52$$ → 减法转换成加法 $$167+(-52)$$ → 负数取 9 的补码表示 $$167+947$$ → 114 进 1 → 高位进的 1 加到低位上去，结果为 115。
    • -52 用 999-52 表示，结果 947，这称为取 9 的补码（9’s Complement）。
      • 参与运算的数的最大位数是 3 位，所以取 9 的补码要用 999（也是 3 位数）去减。
    • 高位进的 1 加到低位上去：本来应该加 1000，结果只加了 1，少加了 999，正好把先前取 9 的补码多加的 999 抵消掉。
    • 67-52 的减法运算变成做 999-52 的减法运算，后者因为没有借位，更容易算。

十进制的 1’s Complement 表示法：负数用 9 的补码表示，减法转换成加法，计算结果的最高位如果有进位则要加回到最低位上去。

要验证规则的正确性，要考虑四种情况：

  1. 两个正数，相加得正；
  2. 一正一负，相加得正；
    • 上例中得到验证。
  3. 一正一负，相加得负；
  4. 两个负数，相加得负。

上述规则也适用于二进制：负数用 1 的补码（1’s Complement）表示，减法转换成加法，计算结果的最高位如果有进位则要加回到最低位上去。

  • 取 1 的补码更简单，$$1-1=0$$，$$1-0=1$$，即取 1 的补码就是把每个 bit 取反。
    • 1 的补码也称为反码。
  • $$00001000-00000100$$ → $$00001000+(-00000100)$$ → $$00001000+11111011$$ → 00000011 进 1 → 高位进的 1 加到低位上去，结果为 00000100。

1’s Complement 表示法相对于 Sign and Magnitude 表示法的优势：

  • 省去了减法器电路，只要有一套加法器电路和一套对每个 bit 取反的电路，就可以做加法和减法运算。
  • 不需单独考虑符号和绝对值，正数和负数的加法都一样算，计算逻辑更简单。
  • 8 个 bit 采用 1’s Complement 表示法表示时，负数的取值范围是从 10000000 到 11111111（-127~0），正数是从 00000000 到 01111111（0~127），仍然可以根据最高位判断正负。

缺点是 0 的表示仍然不唯一，既可以表示成 11111111 也可以表示成 00000000。

  • 为了解决最后这一问题，引入 2’s Complement 表示法。

2’s Complement 表示法

2’s Complement 表示法：正数补码即正数本身，负数补码是该负数的绝对值的原码的每一个二进制位都取反，再加 1。


 00010000   (16 的补码)            11111000    (-8 的补码)
+11111000   (-8 的补码)           +11111000    (-8 的补码)
---------                        ---------
 00001000   (8 的补码)             11110000    (-16 的补码)

  • 2’s Complement 的本质：$$负数 = 0 - 该负数的绝对值$$，不够减就借位。

    
 00000000   (0)            
-00001000   (8)           
            (-8)

# 发生借位，实际被减数是 100000000，100000000 = 11111111 + 1
 100000000
- 00001000
----------
 11111000

# 上一步等价于一下两步
 11111111   # 对应取反步骤
-00001000
---------
 11110111   # 对应加 1 步骤
+00000001
---------
 11111000

  • 计算机内部采用（对应正数的）2 的补码（Two’s Complement）表示负数。

    • 正数的原码、反码、补码的最高位都是 0，所以最高位为 1 的一定是以某种码表示的负数。
    • 计算机读到最高位是 1 的数，知道该数是负数，而负数是以补码形式存储的，所以它将其当补码处理。

8 个 bit 用 2’s Complement 表示法表示时：

  • 负数的取值范围是从 10000000（-128） 到 11111111（-128~-1），正数是从 00000000 到 01111111（0~127）；
  • 可以根据最高位判断一个数是正是负；
  • 0 的表示是唯一的。

溢出判断：在相加过程中最高位产生的进位和次高位产生的进位如果相同则没有溢出，如果不同则表示有溢出。

  • 两个正数相加溢出，结果一定是负数（最高位一定进位成了 1）。
  • 两个负数相加溢出，结果一定是正数（最高位一定变为 0，最高位加一的位置进位成了 1）。
  • 一正一负相加，无论结果是正是负都不可能溢出。
  • 逻辑电路的实现可以把这两个进位连接到一个异或门，把异或门的输出连接到溢出标志位。

计算机做加法时并不区分操作数是有符号数还是无符号数，计算过程都一样。

  • 计算机的加法器在做完计算之后，根据最高位产生的进位设置进位标志，同时根据最高位和次高位产生的进位的异或设置溢出标志。
  • 加法到底是有符号数加法还是无符号数加法则取决于程序如何理解：
    • 如果程序把它理解成有符号数加法，下一步就要检查溢出标志。
    • 如果程序把它理解成无符号数加法，下一步就要检查进位标志。
      • 所以无符号整数默认会 wrap around。
  • 通常计算机在做算术运算之后还可能设置另外两个标志，如果计算结果的所有 bit 都是零则设置零标志，如果计算结果的最高位是 1 则设置负数标志，如果程序把计算结果理解成有符号数，也可以检查负数标志判断结果是正是负。

References