概览

重要密码学技术：

  1. 对称密码（symmetric cryptography）：加密和解密时使用同一密钥。
  2. 公钥密码（public-key cryptography）：加密和解密时使用不同密钥，也叫非对称密码（asymmetric cryptography）。
  3. 混合密码系统（hybrid cryptosystem）：结合了对称密码和公钥密码的优势。
  4. 单向散列函数（one-way hash function）：用于保证完整性（integrity，检测数据是否被篡改）。
    • 无法保证机密性，因为无法还原完整的内容。
  5. 消息认证码（message authentication code）：用于保证完整性并提供认证（authentication）机制，即不但能确认消息是否被篡改，而且能确认消息是否是来自所期待的通信对象。
  6. 数字签名（digital signature）：将现实世界的签名和签章移植到数字世界，用于确保完整性、提供认证、防止抵赖。
  7. 伪随机数生成器（pseudo random number generator，PRNG）：一种能够模拟产生随机数列的算法。

隐写术（steganography）隐藏消息本身（如藏头诗）。

  • 数字水印技术（将著作拥有者及购买者的信息嵌入文件中的技术）运用了隐写术。
  • 实际使用中常将密码与隐写术结合使用。

密码与信息安全常识

  1. 不使用保密的密码算法；
    • 密码算法的安全性只能通过事实说话。将密码算法和代码实现等详细信息交由专业密码破译者，并提供大量的明文和密文文本，即使这样破译一段新的密文仍需相当长的时间，才能说明密码强度高。
    • 通过对密码算法本身进行保密来确保安全性，称为隐蔽式安全性（security by obscurity）。
  2. 使用低强度的密码比不进行任何加密更危险；
    • 这主要是由于用户容易通过“密码”一词获得错误的安全感，导致在处理机密信息时疏忽大意。
  3. 任何密码总有一天会被破解；
    • 一次性密码本除外。
  4. 密码只是信息安全的一部分。

密码学概念

凯撒密码通过将明文中使用的字母按照一定的字数平移来加密。

简单替换密码（simple substitution cipher）指将明文中所使用的字母表替换为另一套字母表的密码。

密钥空间（keyspace）指一种密码能使用的所有密钥的集合。

暴力破解（brute-force attack）指将所有可能的密钥都试一遍，又称穷举搜索（exhaustive search）。

频率分析利用明文中字母的出现频率与密文中字母的出现频率一致这一特性，通过统计密文中每个字母出现的频率和一般文章中所使用的的字母的频率，建立起明文字母和密文字母之间的对应关系。

凯撒密码可以通过暴力破解；简单替换密码很难直接暴力破解，可以用频率分析的破解方法。

密码算法需要重复使用，密钥是可变部分。

  • 每个人都可以拥有相同品牌的锁，但每个人都有不同的钥匙；锁的设计是公开的，但钥匙是私密的。

对称密码

计算机的操作对象并是由 0 和 1 排列而成的比特序列。

各种现实中的对象通过编码（encoding）映射为比特序列。

加密操作就是将表示明文的比特序列转换为表示密文的比特序列。

绝对安全的一次性密码本

XOR（exclusive or，异或）运算中，将 0 理解为偶数，将 1 理解为奇数，则可以将 XOR 和一般的加法运算等同起来，只不过 XOR 不需要进位。

0 ⊕ 0 = 0         偶数（0） + 偶数（0） = 偶数（0）
0 ⊕ 1 = 1         偶数（0） + 奇数（1） = 奇数（1）
1 ⊕ 0 = 1         奇数（1） + 偶数（0） = 奇数（1）
1 ⊕ 1 = 0         奇数（1） + 奇数（1） = 偶数（0）
  • 两个相同的数进行 XOR 运算结果一定是 0。
  • A⊕B⊕B 又能得到 A，和加解密十分相似。
  • 选择合适的 B，仅使用 XOR 就可以实现一个高强度的密码。

一次性密码本（one-time pad）的原理是将明文与一串随机的比特序列进行 XOR 运算。

一次性密码本无法破译，在于无法判断破译出的结果是否是正确的明文。

  • 在对一次性密码本进行暴力破解的过程中，所有的比特排列组合都会出现。
  • 一次性密码本是无条件安全（unconditionally secure），理论上无法破译（theoretically unbreakable）。

一次性密码本的问题：

  1. 密钥的配送；
    • 密钥和明文等长，能安全发送密钥，就能安全发送明文，无需加密后再发送。
  2. 密钥的保存；
    • 密钥和明文等长，能安全保存密钥，就能安全保存明文，从一开始就无需加密再保存。
  3. 密钥的重用；
    • 不能重用随机比特序列，假如泄露，过去用同一个密钥加密的内容也能被解密。
  4. 密钥的生成。
    • 需要生成大量的无重现性的随机数，不能是通过计算机程序生成的伪随机数。

DES, 3DES

DES（Data Encryption Standard）是一种将 64 比特明文加密成 64 比特密文的对称密码算法，不考虑填充的情况下明文和密文等长。

DES 密钥长度是 64 比特，每隔 7 比特会设置一个用于错误检查的比特，因此实质上其密钥长度是 56 比特。

  • 密钥和子密钥的关系？
    • 密钥长度需要乘以轮次，还是不需要乘以轮次、每轮的子密钥由同一个密钥衍生出来

DES 的基本结构称为 Feistel 网络。Feistel 网络中加密的各个步骤称为轮（round），每一轮都需要使用一个不同的子密钥。子密钥（subkey）只在一轮中使用，是一个局部密钥。整个加密过程就是进行若干次轮的循环。

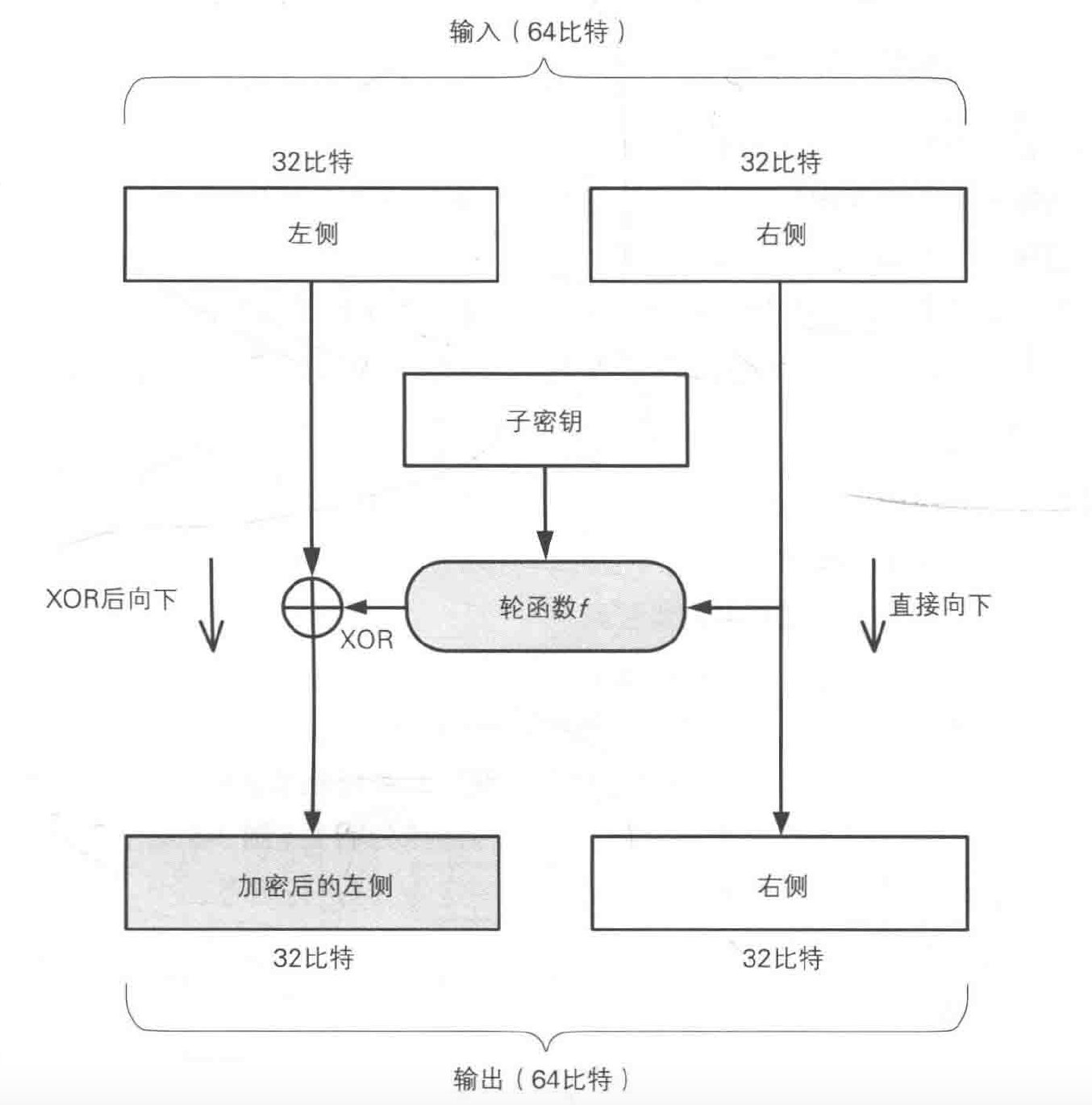
一轮的具体计算步骤：

  1. 将输入的数据（64 比特）等分为左右两部分；
  2. 将输入的右侧（明文）直接发送到输出的右侧；
  3. 将输入的右侧发送到轮函数，轮函数根据右侧（明文）数据和子密钥，计算出一串比特序列；
  4. 将上一步得到的比特序列与左侧数据进行 XOR 运算，并将结果作为加密后的左侧。

轮函数的作用是根据右侧和子密钥生成对左侧进行加密的比特序列，是密码系统的核心。

一轮下来，输入的右侧并没有被加密，因此需要对调左侧和右侧数据并重复若干轮，每一轮用不同的子密钥。

  • 对调只在两轮之间进行，最后一轮结束之后不再对调。

将一轮加密的输出结果用相同的子密钥重新运行一次（不交换），可以发现无论轮函数的集体算法是什么，都可以将密文正确地还原为明文（A⊕B⊕B = A）。所以只要把加密时使用的各个子密钥，按相反的顺序代入同一个 Feistel 网络，就可以完成解密；Feistel 网络本身的结构在加密和解密时是完全相同。

Feistel 网络的性质：

  1. 轮数可以任意增加；
  2. 加密时无论使用何种函数作为轮函数都可以正确解密；
    • 即便用函数的输出结果无法逆向计算出输入的值（即该函数不存在反函数）也没有问题。
    • 轮函数可以无需考虑解密的问题，可以被设计成任意复杂。Feistel 网络实际上就是从加密算法中抽取出密码的本质部分并将其封装成一个轮函数，只要使用 Feistel 网络，就能够保证一定可以解密，因此设计密码算法的人只要努力设计出足够复杂的算法。
  3. 加密和解密用完全相同的结构来实现。
    • Feistel 网络的一轮中，右半部分没有进行任何处理，这在加密算法中看起来是一种浪费，但却保证了可解密性，因为完全没有进行任何处理的右半部分，是解密过程中所必需的信息。
    • 加密和解密可以用完全相同的结构来实现，因此用于实现 DES 算法的硬件设备的设计也变得容易。

DES 已经可以暴力破解，不应再用于任何新的用途。

差分分析是一种针对分组密码的分析方法，其思路是“改变一部分明文并分析密文如何随之改变”。理论上说，即便明文只改变一个比特，密文的比特排列也应该发生彻底的改变，于是通过分析密文的变化，可以获得破译密码的线索。

线性分析的思路是“将明文和密文的一些对应比特进行 XOR 并计算其结果为零的概率”。如果密文具备足够的随机性，则任选一些明文和密文的对应比特进行 XOR 结果为零的概率应该为 $$\frac 1 2$$。如果能够找到大幅偏离 $$\frac 1 2$$ 的部分，则可以借此获得一些与密钥有关的信息。

  • 使用线性分析法，对于 DES 只需要 $$2^{47}$$ 组明文和密文就能够完成破解，相比需要尝试 $$2^{56}$$ 个密钥的暴力破解来说，所需的计算量大幅减少。

差分分析和线性分析都有一个前提，即密码破译者可以选择任意明文并得到其加密结果，这种攻击方式称为选择明文攻击（Chosen Plaintext Attack，CPA）。

三重 DES（triple-DES）是为了增加 DES 强度，将 DES 重复 3 次得到的一种密码算法，也称为 TDEA（Triple Date Encryption Algorithm），通常缩写为 3DES。

明文经过三次 DES 处理才能变成最后的密文，三重 DES 的密钥长度是 $$56×3=168$$ 比特。

三重 DES 并不是进行三次 DES 加密，而是加密→解密→加密的过程。IBM 公司这样设计的目的是为了让三重 DES 能够兼容普通的 DES，用 3 个相同的 DES 密钥组成 3DES 的密钥，这样一来以前用 DES 加密的密文就可以通过 3DES 来解密。

密钥一、密钥三使用相同密钥，密钥二使用不同密钥的 3DES 称为 DES-EDE2，三个密钥全部不同的 3DES 称为 DES-EDE3。

3DES 也不应再用于任何新的用途。

AES

AES（Advanced Encryption Standard）是取代前任标准 DES 成为新标准的一种对称密码算法，全世界的企业和密码学家提交了多个对称密码算法作为 AES 的候选，最终在 2000 年选出了名为 Rijndael 的对称密码算法，并将其确定为 AES。

Rijndael 算法也由多个轮构成，每一轮分为 SubBytes、ShiftRows、MixColumns 和 AddRoundKey 共 4 个步骤。
Rijndael 使用了 SPN 结构。
Rijndael 的输入分组为 128 比特（16 字节）。

Rijndael 加密过程（4×4 矩阵）：

  1. SubBytes 处理：以每个输入的字节的值（O～255 的任意值）为索引，从一张拥有 256 个值的替换表（S-Box）中查找出对应值进行逐个替换；
  2. ShiftRows 平移行处理：将以 4 字节为单位的行（row）按照一定的规则向左平移，且每一行平移的字节数不同；
  3. MixColumns 混合列处理：对一个 4 字节的列进行比特运算，将其变为另外一个 4 字节值；
  4. AddRoundKey 矩阵运算处理：将 MixColumns 的输出与轮密钥进行 XOR；
  5. 重复进行 10 ～ 14 轮计算。

http://www.formaestudio.com/rijndaelinspector/archivos/Rijndael_Animation_v4_eng-html5.html

Rijndael 加密得到的密文和明文等长（16 字节）。

Rijndael 中输入的所有比特在每一轮中都会被加密，相比之加密一半输入的 Feistel 网络的优势是加密所需的轮数更少。另一个优势是 SubBytes、ShiftRows 和 MixColumns 可以分别以字节、行和列为单位进行并行计算。

解密时则按照相反的顺序进行：AddRoundKey → invMixColumns → invSbiftRows → invSubBytes

  • AddRoundKey 是与轮密钥进行 XOR 运算，这一步在加密和解密时完全相同，剩下的步骤的名称都带有 inv 前缀，表示与原始步骤相对应的逆运算。

Rijndael 的分组长度和密钥长度可以分别以 32 比特为单位在 128 比特到 256 比特范围内进行选择。

  • 在 AES 的规格中，分组长度固定为 128 比特，密钥长度只有 128、192 和 256 比特三种。

AES 是推荐使用的对称密码。

密钥配送问题

对称密钥存在密钥配送问题（key distribution problem），即如何在通信双方之间安全地传递密钥。

密钥配送问题解决方案：

  1. 事先共享密钥；
    • 对称密码需要两两之间生成密钥，若参与方很多，密钥数量会很多。
  2. 通过密钥分配中心来解决；
    • 操作流程：
      1. A 向分配中心发出与 B 通信的请求；
      2. 分配中心通过伪随机数生成器生成一个会话密钥，用 A 的密钥将会话密钥加密并将得到的密文发送给 A，用 B 的密钥将会话密钥加密并将得到的密文发送给 B；
      3. A 用解密得到的会话密钥对要发送的消息进行加密后发给 B；
      4. B 用解密得到的会话密钥对 A 的密文进行解密。
    • 无需两两之间生成密钥，分配中心为只保存每个实体本身的密钥，存在中心化的问题。
  3. 通过 Diffie-Hellman 密钥交换来解决；
  4. 公钥密码。

分组密码的模式

密码算法可以分为分组密码和流密码两种。

  • 流密码（stream cipher）是对数据流进行连续处理的一类密码算法，一般以 1 比特、8 比特或 32 比特等为单位进行加密和解密。
    • 流密码不需要填充。
    • 流密码需要保持内部状态来记录加密的进度。
    • 一次性密码本属于流密码。
  • 分组密码（block cipher）是每次只能处理特定长度的一块数据的一类密码算法，这里的一块称为分组（block），一个分组的比特数称为分组长度（block length）。
    • 几乎所有的对称密码算法，都只能将一个固定长度的分组进行加密。
    • 当需要加密的明文长度超过分组长度时，就需要对密码算法进行迭代，迭代的具体方式称为模式（mode）。
      • 当明文长度不是分组长度的整数倍时，需要在最后一个分组中填充一些数据使其凑满一个分组的长度。
      • 选择的模式不恰当，就无法充分保证机密性。
    • DES 和 AES 都属于分组密码。
    • 分组密码处理完一个分组就结束了，不需要通过内部状态来记录加密的进度。

明文分组指分组密码算法中作为加密对象的明文。明文分组的长度与分组密码算法的分组长度相等。

密文分组指使用分组密码算法将明文分组加密之后得到的密文。

分组密码的主要模式：

  1. ECB 模式：Electronic CodeBook mode（电子密码本模式）
  2. CBC 模式：Cipher Block Chaining mode（密码分组链接模式）
  3. CFB 模式：Cipher FeedBack mode（密文反馈模式）
  4. OFB 模式：Output FeedBack mode（输出反馈模式）
  5. CTR 模式：CounTeR mode（计数器模式）

crypto/cipher/example_test.go

ECB 模式

将明文分割成多个分组并逐个加密的方法称为 ECB 模式。

  • ECB 中明文分组加密之后的结果直接成为密文分组。
  • 使用 ECB 模式加密时，相同的明文分组会被转换为相同的密文分组，可以理解为一个巨大的“明文分组→密文分组”的对应表，因此 ECB 模式也称为电子密码本模式。
  • 每个明文分组都各自独立地进行加解密（弱点）。
  • 观察 ECB 的密文就可以分析出明文中存在怎样的重复组合，并可以以此为线索来破译密码。
  • ECB 模式是所有模式中最简单的一种。

对 ECB 模式的攻击：

  • 如果攻击者能够改变密文分组的顺序（或者复制、删除密文），当接收者对密文进行解密时，由于密文分组的顺序被篡改了，相应的明文分组的顺序也会被改变，这意味着攻击者无需破译密码就能够操纵明文。
    • 这一场景中，攻击者不需要破译密码，也不需要知道分组密码算法，他只要知道哪个分组记录了什么样的数据，比如将代表付款人和收款人的两组密文对调。
    • 可以用消息认证码检测出密文的篡改。

不要使用 ECB 模式。

CBC 模式

CBC 模式将前一个密文分组与当前明文分组的内容混合起来后进行加密。

加密流程：首先将明文分组与前一个密文分组进行 XOR 运算，然后再进行加密。

  • 当加密第一个明文分组时，由于不存在“前一个密文分组”，因此需要事先准备一个长度为一个分组的比特序列来代替“前一个密文分组”，这个比特序列称为初始化向量（Initialization Vector，IV）；一般会在每次加密时都随机生成一个不同的比特序列来作为初始化向量。

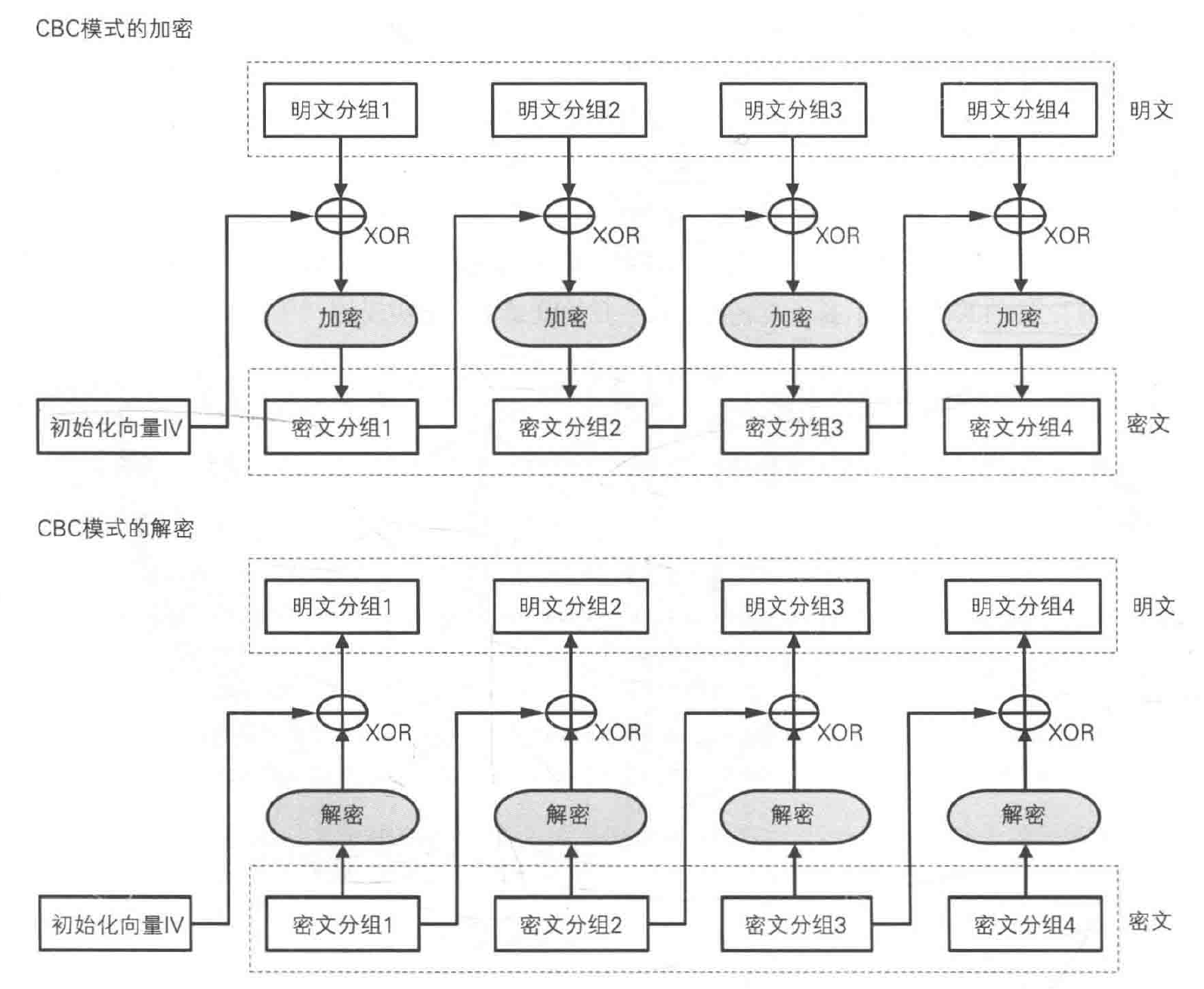
CBC 模式中，无法单独对一个中间的明文分组进行加密，必须要同时得到该明文之前的所有密文分组（链式关系）；只能顺序加密，不能并行加密，可以并行解密。

CBC 模式加密的密文分组中如果有一个分组损坏了，只要密文分组的长度没有发生变化，则解密时最多只会有 2 个分组受到数据损坏的影响；若密文分组中有一些比特缺失了，即便只缺失 1 比特，也会导致密文分组的长度发生变化，此后的分组发生错位，导致缺失比特的位置之后的密文分组全部无法解密。

对 CBC 模式的攻击：

  1. 攻击 IV、修改密文以操纵解密后的明文；
    • 假设攻击者可以使任意（攻击者不能确定是哪个）一个比特反转，攻击者选择反转 IV 中的任意一个比特，密文分组 1 解密的结果与被篡改过的 IV 异或的结果是明文分组 1 中对应的比特也被反转。
      • 若攻击者对密文分组 1 中的任意一个比特进行反转，则明文分组 2 中相应的比特也会被反转，但密文分组 1 中的一比特的反转，会对解密后、异或前的明文分组 1 中的多个不确定的比特造成影响，这样攻击者就不能（很难）使明文分组 1 中的特定比特发生变化。
    • 可以用消息认证码检测出数据的篡改。
  2. 填充提示攻击（Padding Oracle Attack）；
    • 攻击者反复发送一段密文，每次发送时都对填充的数据进行少许改变，接收者（服务器）在无法正确解密时会返回一个错误消息，攻击者通过这一错误消息就可以获得一部分与明文相关的信息。
    • 这一攻击方式适用于所有需要进行分组填充的模式。
  3. 攻击 IV。
    • IV 必须使用不可预测的随机数。SSL/TLS 的 TLS 1.0 版本协议中，IV 并没有使用不可预测的随机数，而是使用了上一次 CBC 模式加密时的最后一个分组。为了防御攻击者对此进行攻击，TLS 1.1 以上的版本改为了必须显式传送 IV。

CBC 模式应用实例：SSL/TLS，3DES_EDE_CBC，AES_256_CBC。

分组密码中还有一种模式叫作 CTS 模式（Cipher Text Stealing）。CTS 模式使用最后一个分组的前一个密文分组数据来填充不足位的最后一个明文分组，通常和 ECB 模式以及 CBC 模式配合使用。

CFB 模式

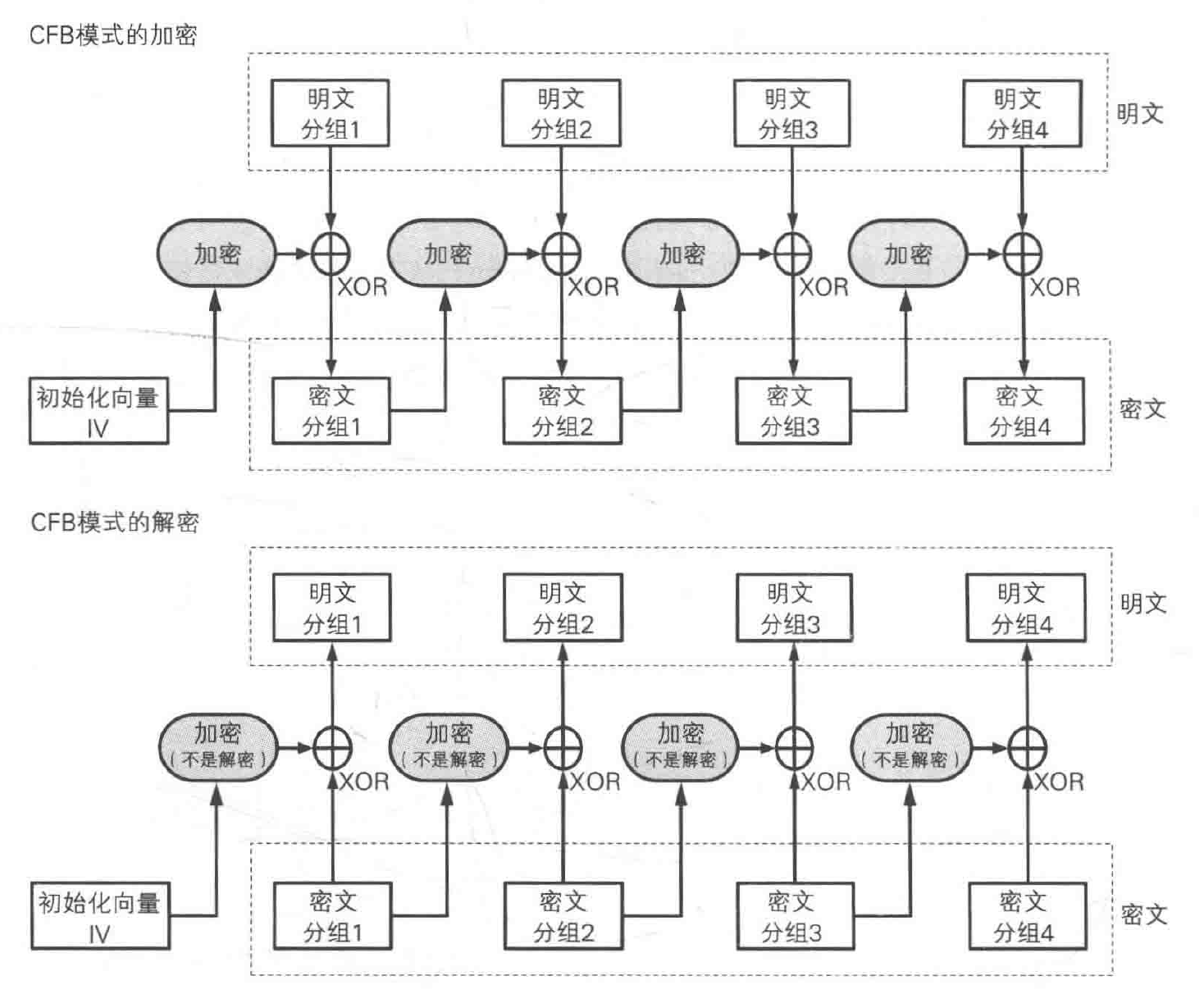
加密过程：前一个密文分组（或者初始化向量）经过加密后的得到的比特序列（称为密钥流）和明文分组进行 XOR 运算，得到密文分组（密钥流⊕明文=>密文）。

  • 只能顺序加密，不能并行加密。

CFB 模式解密时，分组密码算法依然执行加密操作，因为密钥流是通过加密操作来生成的。可以并行解密。

CFB 模式的结构与一次性密码本是非常相似的，一次性密码本通过将明文与随机比特序列进行 XOR 运算来生成密文，CFB 模式则是通过将明文分组与密码算法的输出进行 XOR 运算来生成密文分组。

  • 由于密码算法的输出是通过计算得到的，并不是真正的随机数，因此 CFB 模式不可能像一次性密码本那样具备理论上不可破译的性质。

在 CFB模式中，密码算法相当于用来生成密钥流的伪随机数生成器，而初始化向量就相当于伪随机数生成器的种子。

CFB 模式中，明文数据可以被逐比特加密，因此我们可以将 CFB 模式看作是一种使用分组密码来实现流密码的方式。

对 CFB 模式可以实施重放攻击：

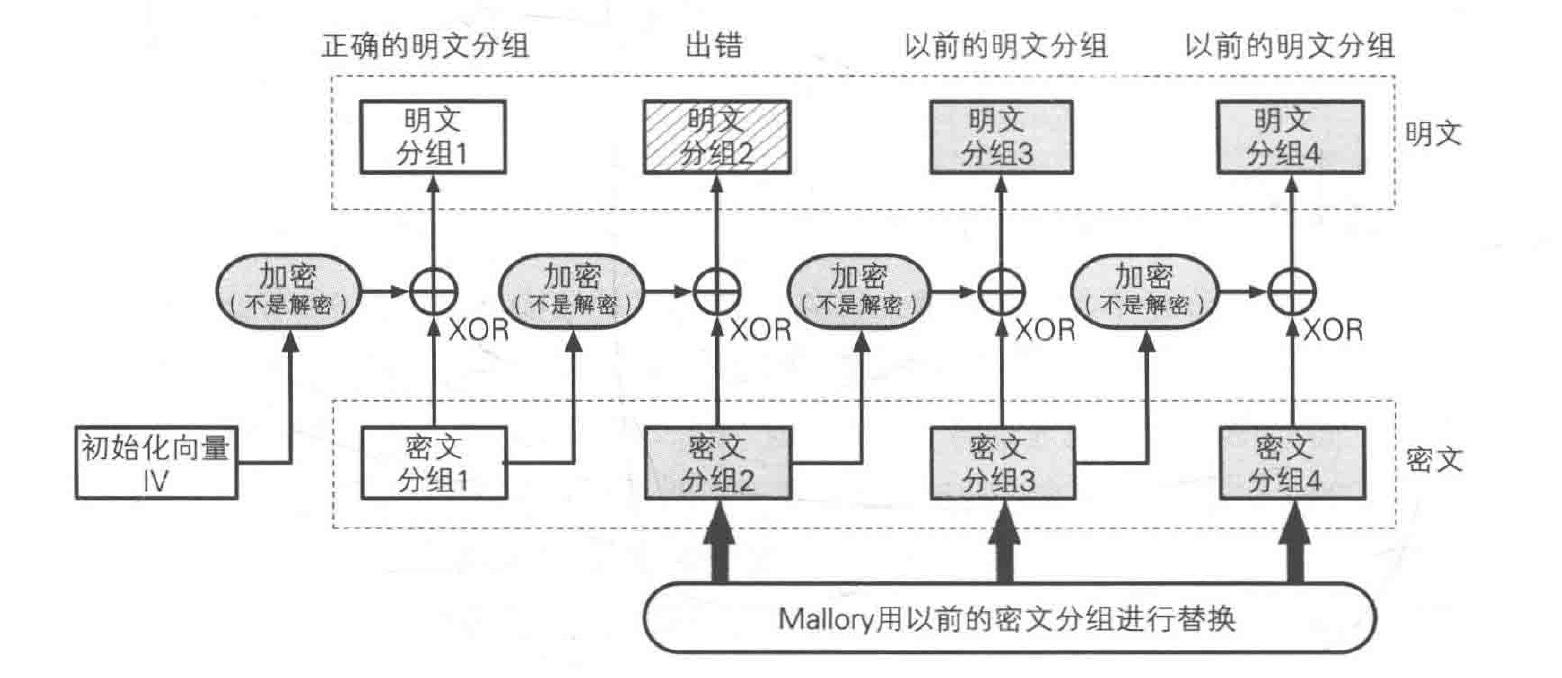
  1. A 向 B 发送由 4 个密文分组组成的一条消息；
  2. 攻击者将消息的后 3 个密文分组保存下来；
  3. A 又向 B 发送内容不同的 4 个密文分组（假设 A 使用相同密钥）；
  4. 攻击者用之前保存下来的 3 个密文分组替换掉第二条消息的后 3 个密文分组；
  5. B 解密第二条消息时，只有第 1 个可以解密成正确的明文分组，第 2 个会出错，第 3 个和第 4 个变成了被替换的内容（第一条消息中的内容）。
    • B 无法判断第 2 个分组出错到底是通信错误还是被攻击造成的，要解决这个问题需要使用消息认证码。

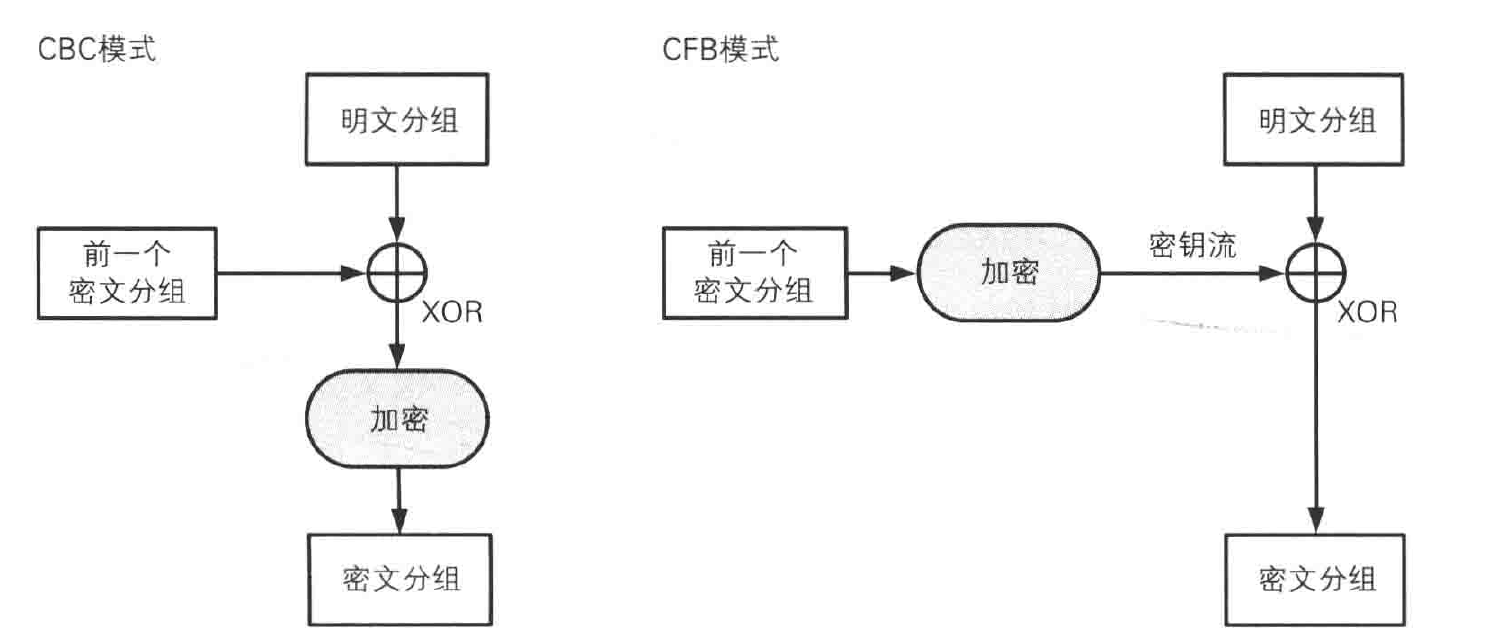
在 ECB 模式和 CBC 模式中，明文分组都是通过密码算法进行加密的；CFB 模式中，明文分组并没有通过密码算法来直接进行加密，明文分组和密文分组之间只有一个 XOR。

OFB 模式

OFB 模式并不是通过密码算法对明文直接进行加密的，而是通过将明文分组和密文算法的输出进行 XOR 产生密文分组，这点上和 CFB 模式很像。

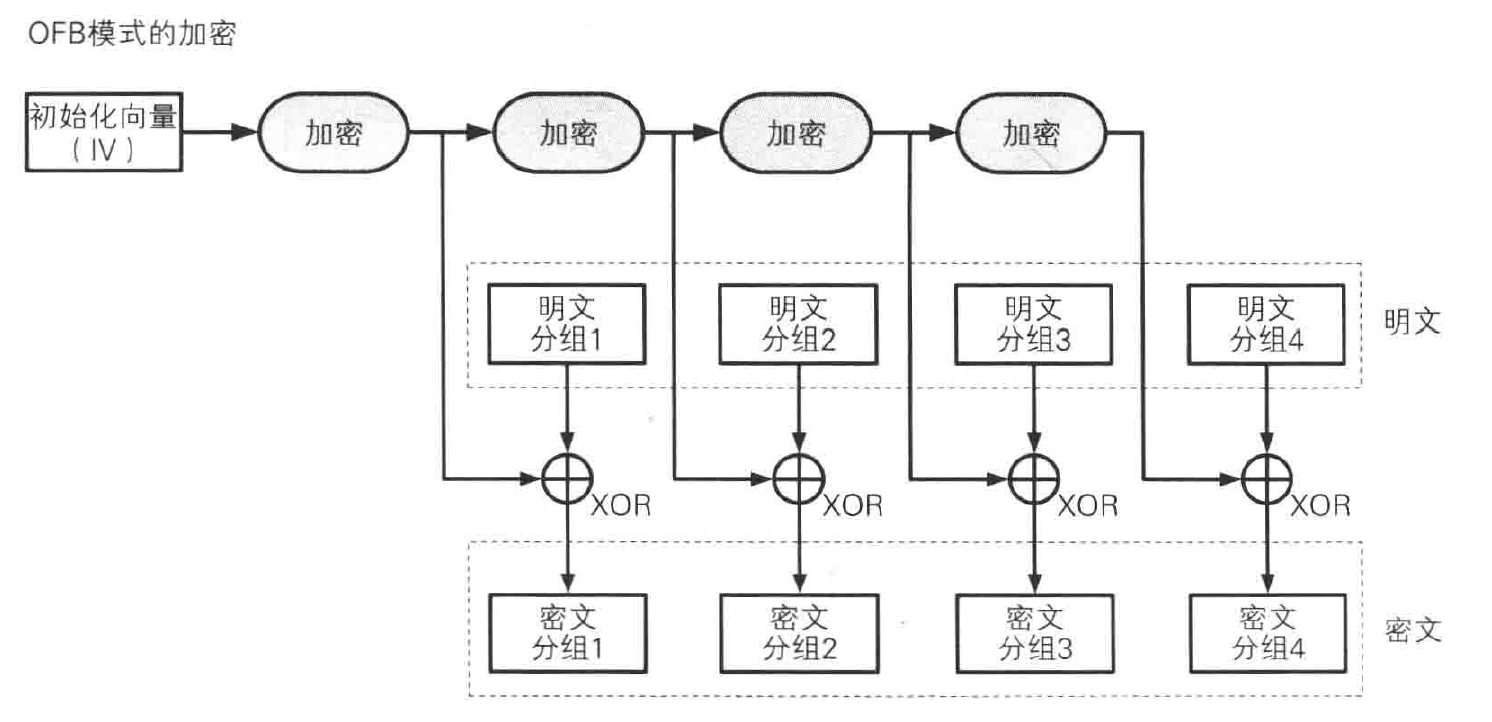
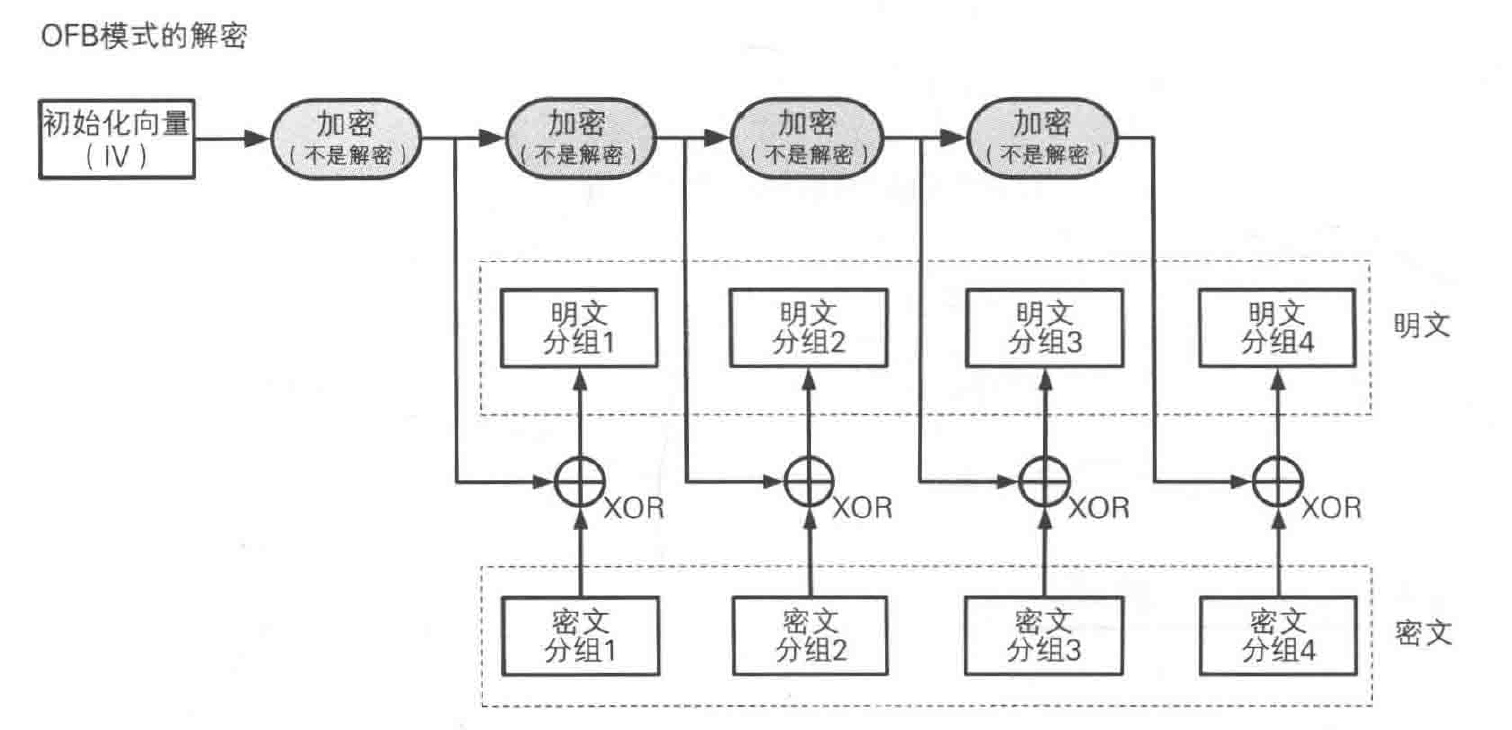
OFB 模式中也需要使用初始化向量（IV）。

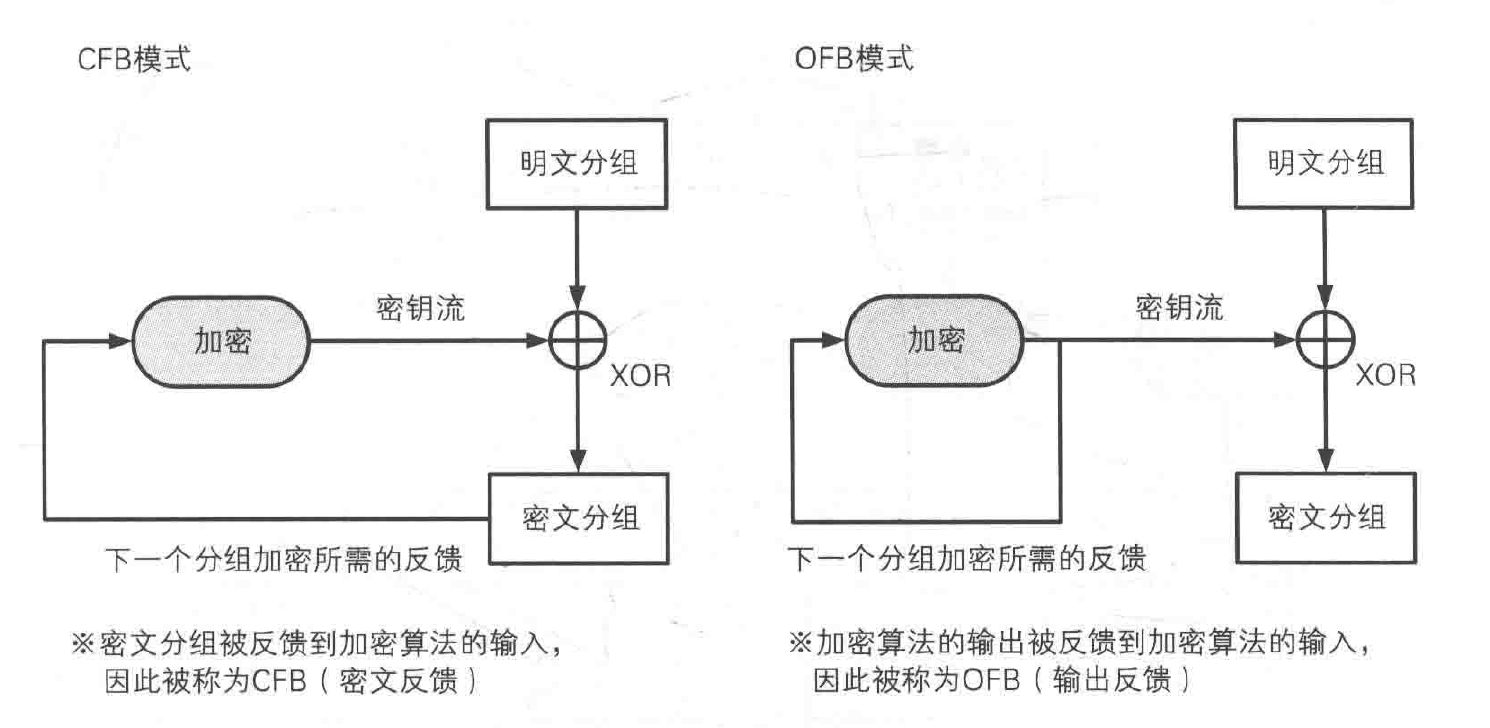
OFB 模式和 CFB 模式的区别仅仅在于密码算法的输入。CFB 模式中，密码算法的输入是前一个密文分组，也就是将密文分组反馈到密码算法中，因此就有了“密文反馈模式”这个名字；OFB 模式中，密码算法的输入则是密码算法的前一个输出（链式结构），也就是将上一个密文输出反馈给密码算法，因此就有了“输出反馈模式”这个名字。

由于 CFB 模式中是对密文分组进行反馈的，因此必须从第一个明文分组开始按顺序进行加密，无法跳过明文分组 1 而先对明文分组 2 进行加密。

OFB 模式中，XOR 所需要的比特序列（密钥流）可以事先通过密码算法生成，和明文分组无关。只要提前准备好所需的密钥流，在实际从明文生成密文的过程中，就不再需要用到密码算法，只要将明文与密钥流进行 XOR 就可以。和 AES 等密码算法相比，XOR 运算速度是非常快的，只要提前准备好密钥流就就可以快速完成加密。这也意味着生成密钥流的操作和进行 XOR 运算的操作可以并行。

CTR 模式

CTR 模式全称是 CounTeR 模式（计数器模式），通过将逐次累加的计数器进行加密来生成密钥流的流密码。

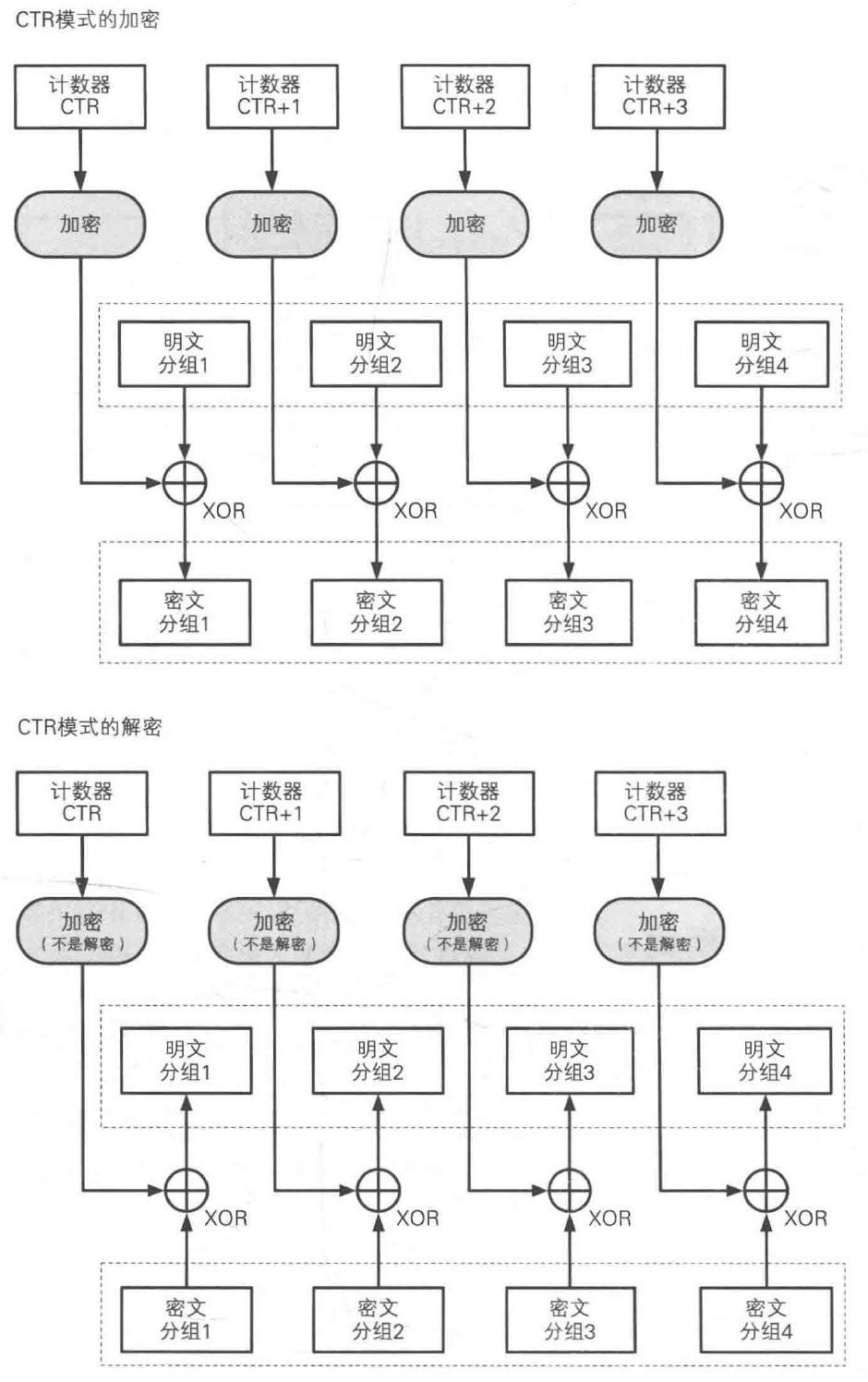
每个分组对应一个逐次累加的计数器，并通过对计数器进行加密来生成密钥流，最终的密文分组通过将计数器加密得到的比特序列，与明文分组进行 XOR 得到。

每个加密周期都会生成一个不同的值 nonce 来作为计数器的初始值。

# 分组长度为 128 比特（16 字节）
66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 01

66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 01     明文分组 1 的计数器（初始值）
66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 02     明文分组 2 的计数器 
66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 03     明文分组 3 的计数器 
66 1F 98 CD 37 A3 8B 4B 00 00 00 00 00 00 00 04     明文分组 4 的计数器
  • 前 8 个字节为 nonce；
  • 后 8 个字节为分组序号，逐次累加。

由于计数器的值每次都不同，因此每个分组中将计数器进行加密所得到的密钥流也不同的，这种方法就是用分组密码来模拟生成随机的比特序列。

CTR 和 OFB 都是流密码。

CTR 模式中可以按任意顺序对分组进行加密和解密，加密和解密时用到的计数器的值可以由 nonce 和分组序号直接计算出来；能够以任意顺序处理分组就意味着能够实现并行计算，在支持并行计算的系统中 CTR 模式的速度非常快。

若 CTR 模式的密文分组中有一个比特被反转了，则解密后明文分组中仅有与之对应的比特会被反转，这一错误不会放大。攻击者可以通过反转密文分组中的某些比特，引起解密后明文中的相应比特也发生反转，这一弱点和 OFB 模式是相同的。

OFB 模式中，如果对密钥流的一个分组进行加密后的结果碰巧和加密前是相同的，那么这一分组之后的密钥流就会以同一值不断重复，CTR 模式中则不存在这一问题。

在 CTR 模式的基础上增加认证功能的模式称为 GCM 模式（Galois/Counter Mode）。这一模式能够在 CTR 模式生成密文的同时生成用于认证的信息，从而能够判断密文是否是由合法的加密过程生成的。通过这一机制，即便主动攻击者发送伪造的密文，也能够识别出密文是伪造的。

公钥密码

公钥密码中，首先要生成一个包含公钥和私钥的密钥对（key pair），公钥和私钥一一对应，数学上决定公钥和私钥不能单独生成，且公钥加密得到的密文只能被对应的私钥解密。

公钥是加密密钥，可以公开，发送者用接收者公钥对消息进行加密；私钥是解密密钥，需私密保存，接收者用自己的私钥对密文进行解密。

时钟运算

除以 12 求余数称为以 12 取模。

27 mod 12 = 3 可以描述成 27 与 3 以 12 为模同余。

对于算式 a × b mod 12 = 1，可以发现 a 和 b 是时钟运算中的倒数（即不考虑 mod 12 部分）。时钟运算中某个数是否存在倒数，可以通过这个数和 12 的最大公约数是否为 1（即是否与 12 互质）这个条件来进行判断。

  • 2 虽然是质数，但在时钟运算中 2 不存在“倒数”，因为无论如何无法满足 2 × ? mod 12 = 1。可以理解为只要以 2 个刻度为单位，无论如何转动指针，都只能指向 0、2、4、6、8、10、0、2、4、6、8 等这些偶数位置，而绝对不会指向 1。此处 b 的范围是 [0, 11]，大于此范围的数对 12 取模后也会落入此范围。

时钟运算中某个数是否存在倒数的问题与公钥算法 RSA 中一个公钥是否存在相对应的私钥的问题直接相关。

\(7^? = 49\)：乘方的逆运算称为对数，即便数字很大，求对数也并不困难。

\(7^? mod 13 = 8\)：时钟运算中的对数称为离散对数，当数字很大时，求离散对数非常困难，也非常耗时，尚未有快速求出离散对数的算法。

RSA

RSA 是一种公钥密码算法，名字由它的三位开发者 Ron Rivest、Adi Shamir 和 Leonard Adleman 的姓氏首字母组成的。

RSA 加密：$$密文 = 明文^E mod\ N$$。

  • E 和 N 的组合就是公钥，E 指 Encryption，N 指 Number。
  • 知道 E 和 N，任何人都可以完成加密运算。

RSA 解密：$$明文 = 密文^D mod\ N$$

  • D 和 N 的组合就是私钥，D 指 Decryption。
  • 解密时使用的 N 和加密时使用 N 是同一个。

RSA 密钥对生成步骤：

  1. 求 N；

    • 准备两个大质数 p，q，假设是 512 比特的155 位的十进制数（太小易破译，太大计算耗时长）。
      • 具体方法是通过伪随机数生成器生成 512 比特大小的数，再判断它是不是质数。
      • 判断一个数是不是质数并不是看它能不能分解质因数，而是通过数学上的判断方法（包括费马测试和米勒·拉宾测试等）。
    • $$N = p × q$$

  2. 求 L（L 是仅在生成密钥对过程中使用的数）；

    • L 是 p-1 和 q-1 的最小公倍数（least common multiple）。
    • $$L = lcm(p-l, q-1)$$

  3. 求 E；

    1 < E < L
gcd(E, L) = 1
    • E 比 1 大、比 L 小；E 和 L 的最大公约数（greatest common divisor）为 1，即 E 和 L 互质（E 相对于 L 是质数，E 本身可以不是质数）。
      • 具体方法是通过伪随机数生成器在 1 < E < L 的范围内生成 E 的候选数，再判断其是否满足 gcd(E, L) = 1 条件。
      • 求最大公约数可以用欧几里得辗转相除法。
    • gcd(E, L) = 1 保证了一定存在解密时需要使用的数 D。
    • 满足条件的 E 可以有多个。

  4. 求 D。

    1 < D < L 
E × D mod L = 1
    • 要保证存在满足 E × D mod L = 1 条件的 D，就需要保证 E 和 L 的最大公约数为 1（这是求 E 时需要满足的一个条件；参考时钟运算中的倒数）。
    • E × D mod L = 1 保证了对密文进行解密时能够得到原来的明文。
    • 如何快速求 D？

质数不会用光，无需考虑生成 RSA 需要的质数组合时发生撞车的情况。

加密的明文必须是小于 N 的数，因为解密运算时也要去求 mod N，mod N 的结果必定小于 N，因此如果明文本身比大 N，解密后必然不能得到正确的明文。
意味着明文大于 N 时需要分组。

crypto/rsa/example_test.go

对 RSA 的攻击

  1. 通过密文来求得明文
    • 破译者知道密文、E 和 N（$$密文 = 明文^E mod\ N$$），若没有 mod N 部分（$$密文 = 明文^E$$ mod N），则是一个求对数问题；加上 mod N 就变成了求离散对数的问题，目前尚未发现求离散对数的高效算法。
  2. 通过暴力破解找出 D
    • 逐一尝试有可能作为 D 的数字，难度会随着 D 的长度增加而变大，当 D 足够长时，就不可能在有现实意义的时间内找出 D。
      • RSA 中使用的 p 和 q 的长度在 1024 比特以上，因此 N 的长度在 2048 比特以上，而 E 和 D 的长度可以和 N 的长度接近，找出 D 需要进行 $$2^{2048}$$ 次以上的尝试。
  3. 通过 E 和 N 求出 D
    • 破译者知道 E 和 N，不知道 p 和 q 的值，因此不可能通过和生成密钥对时相同的计算方法来求出 D（E × D mod L = 1，L = lcm(p-l, q-1)）；p 和 q 的保密至关重要，破译者知道 p 和 q 就相当于知道了私钥，破译者的攻击实际上是对 p 和 q 的破解尝试。
      1. 对 N 进行质因数分解攻击求 p 和 q。目前尚未发现对大整数进行质因数分解的高效算法；尚未证明质因数分解是否非常困难；尚不确定是否存在一种分解质因数的简单方法。
      2. 通过推测 p 和 q 进行攻击。p 和 q 由伪随机数生成器生成，如果伪随机数生成器的算法不安全，破译者就有可能推测出 p 和 q。
      3. 其他攻击。对 N 进行质因数分解求出 p 和 q 后就能求出 D，“求 D” 与“对 N 进行质因数分解”是否等价，需要数学证明（2004 年 Alexander May 证明 “求 D” 与“对 N 进行质因数分解”在确定性多项式时间内等价）。这样的方法目前尚未出现，也不确定是否存在这样的方法。
  4. 中间人攻击（man-in-the-middle attack）
    • 中间人位于通信路径中，能够窃听或篡改邮件的内容，拦截邮件使接收方无法接收到。
    • 攻击步骤：
      1. 发送者 A 向接收者 B 发邮件索要公钥；
      2. B 试图将自己的公钥发给 A 的过程中，中间人 M 拦截 B 的邮件，将 B 的公钥保存下来，并将自己的公钥发给 A；
      3. A 用收到的被替换过的 B 的公钥（实际是 M 的公钥）与 B 进行加密通信；
      4. M 拦截 A 加密过的信息，用自己的私钥解密得到明文，随后 M 任意篡改内容后用保存下来的 B 的公钥对篡改后的内容进行加密，发给 B；
      5. B 解密后拿到的是被 M 篡改过的信息。
  5. 选择密文攻击（chosen ciphertext attack）
    • 假设攻击者发送任意数据（不包括攻击者试图攻击的那一段密文本身），服务器都会将其当作密文来解密并返回解密结果（这种服务称为解密提示，decryption oracle）。攻击者向服务器反复发送自己生成的伪造密文，并通过分析服务器返回的错误消息和响应时间获得一些关于密钥和明文的信息。
    • 选择密文攻击并不能破译 RSA，但攻击者能够获得密文所对应的明文的少量信息。
    • 抵御选择密文攻击的关键是判断密文是否是由知道明文的人通过合法的方式生成。
      • RSA-OAEP（Optimal Asymmetric Encryption Padding，最优非对称加密填充）在加密时会在明文前面填充一些认证信息，包括明文的散列值以及一定数量的 0，然后再对填充后的明文用 RSA 进行加密。在 RSA-OAEP 的解密过程中，如果在 RSA 解密后的数据的开头没有找到正确的认证信息，则可以断定这段密文不是由知道明文的人生成的，并返回一条固定的错误消息。在 RSA-OAEP 的实际运用中，还会通过随机数使得每次生成的密文呈现不同的排列方式。

常用公钥密码

  1. RSA：利用质因数分解的困难度。
  2. EIGamal：利用 mod N 下求离散对数的困难度；经过加密的密文长度会变为明文的两倍。
  3. Rabin：利用了 mod N 下求平方根的困难度。
  4. 椭圆曲线密码（Elliptic Curve Cryptography，ECC）：通过将椭圆曲线上的特定点进行特殊的乘法运算来实现，利用了这种乘法运算的逆运算非常困难这一特性；所需的密钥长度比 RSA 短。

RSA 是公钥密码的事实标准。

由于密码劣化，NIST SP800-57 建议 1024 比特的 RSA 不应被用于新用途；2048 比特的 RSA 可在 2030 年之前被用于新用途；4096 比特的 RSA 在 2031 年之后仍可被用于新用途。

公钥密码的不足

公钥密码的处理速度只有对称密码的几百分之一。

公钥密码存在公钥认证问题，无法确认收到的公钥是否确实是属于你期望与之通信的对象。

混合密码系统

混合密码系统（hybrid cryptosystem）用对称密码来加密明文，提高处理速度；用公钥密码来加密对称密码中使用的密钥（会话密钥），解决密码配送问题。

会话密钥（session key）指为本次通信而生成的临时密钥，一般由伪随机数生成器产生。会话密钥是对称密码的密钥，最多十几个字节，一般比消息明文本身要短，即使公钥加密速度不快，加密一个会话密钥也可以很快完成，比直接加密消息明文快很多。

混合密码系统运用了伪随机数生成器、对称密码和公钥密码，其中每一种技术要素的强度都必须很高，而且这些技术要素之间的强度平衡也非常重要。

  • 如果伪随机数生成器的算法很差，生成的会话密钥就有可能被攻击者推测出来；会话密钥中哪怕只有部分比特被推测出来也很危险，因为会话密钥的密钥空间不大，很容易被暴力破解。
  • 同时需要使用高强度的对称密码算法和公钥密码算法，并确保密钥具有足够的长度，无论其中任何一方的密钥过短，都可能遭到集中攻击，因此对称密码和公钥密码的密钥长度必须具备同等强度。
    • 考虑到长期使用的情况，公钥密码的强度应高于对称密码，因为对称密码的会话密钥被破译只会影响本次通信的内容，而公钥密码一旦被破译，从过去到未来用相同公钥加密的所有通信内容就都被破译了。

具备同等抵御暴力破解强度的密钥长度比较：

对称密码 AES 公钥密码 RSA
128 3072
192 7680
256 15360

References